四种命题（四） 人教选修1-1

四种命题（四） 人教选修1-1,标签：高三数学教学设计案例,http://www.5ijcw.com

   即，  ∴   (推理利用了不等式的传递性)．

又由  ∴ ，但这些都与已知条件矛盾．

∴  成立．

例2：用反证法证明：圆的两条不是直径的相交弦不能互相平分．

已知：如图：在⊙0中，弦AB、CD交于点P，且AB、CD不是直径．

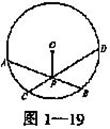
www.5ijcw.com 求证：弦AB、CD不被P平分．

证明：假设弦AB、CD被P平分，连结OP，由平面几何知识可推出：

OP⊥AB且OP⊥CD

又推出：在平面内过一点P有两条直线

AB和CD同时与OP垂直，这与垂线性质矛盾，则原命题成立．

由上述两例题可看：利用反证法证明时，关键是从假设结论的反面出发，经过推理论证，得出相矛盾的结论，这是由假设所引起的，因此这个假设是不正确的，从而肯定了命题结论的正确性．

反证法证题的关键是：第二步即从结论的反面出发，经过推理论证，得出矛盾．反证法引出的矛盾有以下几种情况：

（1）与原题中的条件矛盾；

（2）与定义、公理、定理、公式等矛盾；

（3）与假设矛盾．

例3：若p>0,q>0,p³+p³=2.试用反证法证明：p+q≤2．

分析：此题直接由条件推证p+q≤2是较难的，由此用反证法证之．

证明：假设p+q>2,

∵p>0,q>0.

（p+q）³=p³+3p²q+3pq²+q³>8.

又∵p³

上一页  [1] [2] [3] [4]  下一页

上一篇：四种命题（三） 人教选修1-1